1.4 Trigonometric Functions
We begin our trigonometric review by recalling the two systems of angle measurement: radians and degrees. They are best described using the relationship between angles and rotation. As is customary, we often use the lowercase Greek letter \(\theta\) (“theta”) to denote angles and rotations.
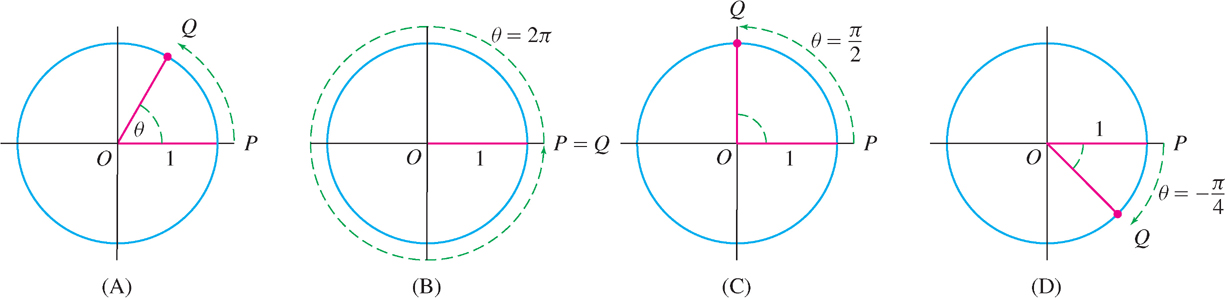
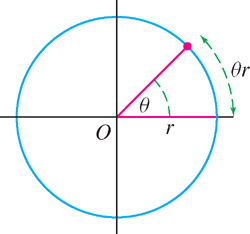
Figure 1.39(A) shows a unit circle with radius \(\overline{OP}\) rotating counterclockwise into radius \(\overline{OQ}\). The radian measure of this rotation is the length \(\theta\) of the circular arc traversed by \(P\) as it rotates into \(Q\). On a circle of radius \(r\), the arc traversed by a counterclockwise rotation of \(\theta\) radians has length \(\theta r\) (Figure 1.40).
The unit circle has circumference \(2\pi\). Therefore, a rotation through a full circle has radian measure \(\theta = 2\pi \) [Figure 1.39(B)]. The radian measure of a rotation through one-quarter of a circle is \(\theta = 2\pi /4 = \pi /2\) [Figure 1.39(C)] and, in general, the rotation through one-\(n^{\text{th}}\) of a circle has radian measure \(\frac{2\pi}{n}\) (Table 1.5). A negative rotation (with \(\theta \lt 0\)) is a rotation in the clockwise direction [Figure 1.39(D)]. The unit circle has circumference \(2\pi\) (by definition of the number \(\pi \)).
| Rotation through | Radian measure |
|---|---|
| Two full circles | \(4\pi\) |
| Full circle | \(2\pi \) |
| Half circle | \(\pi \) |
| Quarter circle | \(\frac{2\pi}{4}=\frac{\pi}{2}\) |
| One-sixth circle | \(\frac{2\pi}{6}=\frac{\pi}{3}\) |
The radian measure of an angle such as \(\angle POQ\) in Figure 1.39(A) is defined as the radian measure of a rotation that carries \(\overline{OP}\) to \(\overline{OQ}\). Notice, however, that the radian measure of an angle is not unique. The rotations through \(\theta\) and \(\theta + 2\pi \) both carry \(\overline{OP}\) to \(\overline{OQ}\). Therefore, \(\theta\) and \(\theta + 2\pi \) represent the same angle even though the rotation through \(\theta + 2\pi \) takes an extra trip around the circle. In general, two radian measures represent the same angle if the corresponding rotations differ by an integer multiple of \(2\pi\). For example, \(\frac{\pi}{4}\), \(\frac{9\pi}{4}\), and \(-\frac{15\pi}{4}\) all represent the same angle because they differ by multiples of \(2\pi \):
\[ \frac{\pi}{4}=\frac{9\pi}{4}-2\pi=-\frac{15\pi}{4}+4\pi \]
Every angle has a unique radian measure satisfying \(0 \leq \theta \lt 2\pi \). With this choice, the angle \(\theta\) subtends an arc of length \(\theta r\) on a circle of radius \(r\) (Figure 1.40).
Degrees are defined by dividing the circle (not necessarily the unit circle) into \(360\) equal parts. A degree is \(\frac{1}{360}\) of a circle. A rotation through \(\theta\) degrees (denoted \(\theta^{\circ}\)) is a rotation through the fraction \(\frac{\theta}{360}\) of the complete circle. For example, a rotation through \(90^{\circ}\) is a rotation through the fraction \(\frac{90}{360}\), or \(\frac{1}{4}\), of a circle.
As with radians, the degree measure of an angle is not unique. Two degree measures represent that same angle if they differ by an integer multiple of \(360\). For example, the angles \(-45^{\circ}\) and \(675^{\circ}\) coincide because \(675 = -45 + 2(360)\). Every angle has a unique degree measure \(\theta\) with \(0 \leq \theta < 360\).
| Radians | Degrees |
|---|---|
| \(0\) | \(0^{\circ}\) |
| \(\frac{\pi}{6}\) | \(30^{\circ}\) |
| \(\frac{\pi}{4}\) | \(45^{\circ}\) |
| \(\frac{\pi}{3}\) | \(60^{\circ}\) |
| \(\frac{\pi}{2}\) | \(90^{\circ}\) |
To convert between radians and degrees, remember that \(2\pi\text{ rad}\) is equal to \(360^{\circ}\). Therefore, \(1\text{ rad}\) equals \(\frac{360}{2\pi}\) or \(\frac{180}{\pi}\) degrees.
- To convert from radians to degrees, multiply by \(\frac{180}{\pi}\).
- To convert from degrees to radians, multiply by \(\frac{\pi}{180}\).
26
EXAMPLE 1
Radian measurement is usually the better choice for mathematical purposes, but there are good practical reasons for using degrees. The number \(360\) has many divisors \((360 = 8\cdot9\cdot5)\), and consequently, many fractional parts of the circle can be expressed as an integer number of degrees. For example, one-fifth of the circle is \(72^{\circ}\), two-ninths is \(80^{\circ}\), three-eighths is \(135^{\circ}\), etc.
Convert (a) \(55^{\circ}\) to radians and (b) \(0.5\text{ rad}\) to degrees.
Solution
(a) \(55^{\circ}\times\frac{\pi}{180}\approx0.9599\text{ rad}\)
(b) \(0.5\text{ rad}\times\frac{180}{\pi}\approx28.648^{\circ}\)
Convention: Unless otherwise stated, we always measure angles in radians.
The trigonometric functions \(\sin \theta\) and \(\cos \theta\) can be defined in terms of right triangles. Let \(\theta\) be an acute angle in a right triangle, and let us label the sides as in Figure 1.41. Then
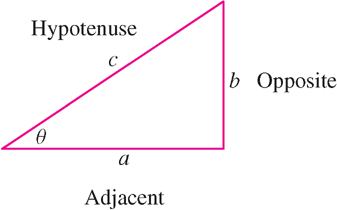
\[\boxed{ \sin\theta=\frac{b}{c}=\frac{\text{opposite}}{\text{hypotenuse}},\quad \cos\theta=\frac{a}{c}=\frac{\text{adjacent}}{\text{hypotenuse}} } \]
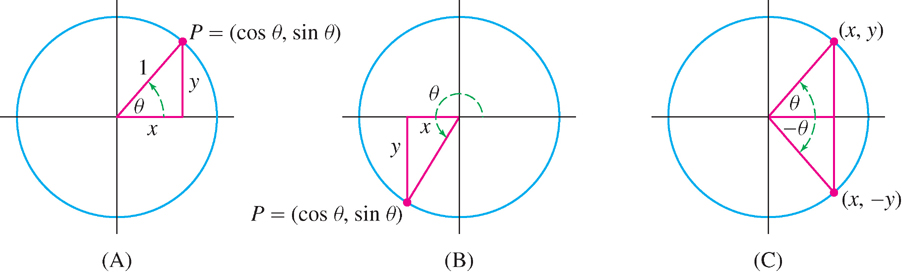
A disadvantage of this definition is that it makes sense only if \(\theta\) lies between \(0\) and \(\frac{\pi}{2}\) (because an angle in a right triangle cannot exceed \(\frac{\pi}{2}\)). However, sine and cosine can be defined for all angles in terms of the unit circle. Let \(P = (x, y)\) be the point on the unit circle corresponding to the angle as in Figure 1.42(A) and (B), and define
\[ \cos \theta = x\text{-coordinate of }P,\quad \sin \theta = y\text{-coordinate of }P \]
This agrees with the right-triangle definition when \(0<\theta<\frac{\pi}{2}\). On the circle of radius \(r\) (centered at the origin), the point corresponding to the angle \(\theta\) has coordinates
\[ (r\cos\theta, r\sin\theta) \]
Furthermore, we see from Figure 1.42(C) that \(\sin \theta\) is an odd function and \(\cos \theta\) is an even function:
\[\boxed{ \sin(-\theta)=-\sin\theta,\quad \cos(-\theta)=\cos\theta } \]
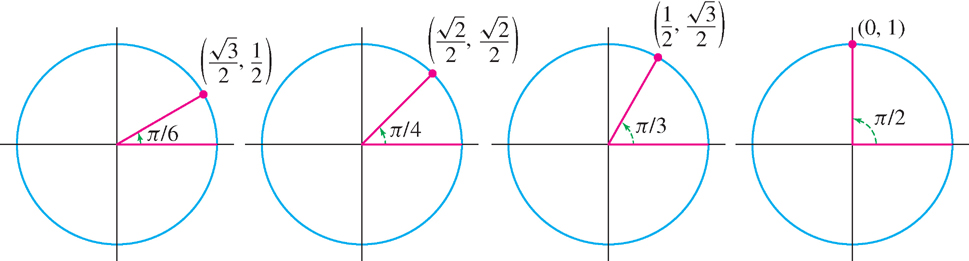
Although we use a calculator to evaluate sine and cosine for general angles, the standard values listed in Figure 1.43 and Table 1.6 appear often and should be memorized.
27
| \[ \begin{gathered} \text{Table 1.6}\\ \begin{array}{|r|ccccccccc|} \hline \theta&0&\frac{\pi}{6}&\frac{\pi}{4}&\frac{\pi}{3}&\frac{\pi}{2}&\frac{2\pi}{3}&\frac{3\pi}{4}&\frac{5\pi}{6}&\pi\\[5pt] \hline \sin\theta&0&\frac{1}{2}&\frac{\sqrt{2}}{2}&\frac{\sqrt{3}}{2}&1&\vphantom{-}\frac{\sqrt{3}}{2}&\vphantom{-}\vphantom{-}\frac{\sqrt{2}}{2}&\frac{1}{2}&\vphantom{-}0\\[5pt] \hline \cos\theta&1&\frac{\sqrt{3}}{2}&\frac{\sqrt{2}}{2}&\frac{1}{2}&0&-\frac{1}{2}&-\frac{\sqrt{2}}{2}&-\frac{\sqrt{3}}{2}&-1\\ \hline \end{array} \end{gathered} \] |
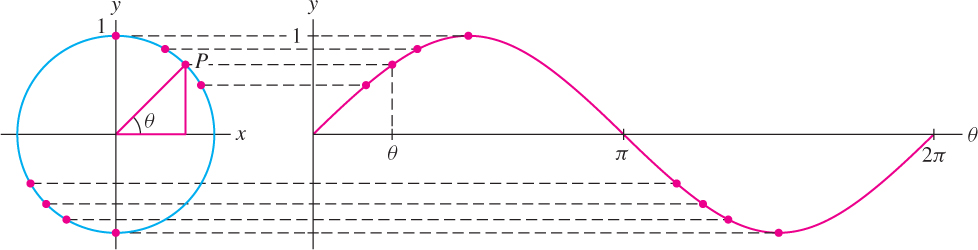
The graph of \(y = \sin \theta\) is the familiar “sine wave” shown in Figure 1.44. Observe how the graph is generated by the y-coordinate of the point P = (cos \theta, sin \theta) moving around the unit circle.
The graph of \(y = \cos \theta\) has the same shape but is shifted to the left \(\frac{\pi}{2}\) units (Figure 1.45). The signs of \(\sin \theta\) and \(\cos \theta\) vary as \(P = (\cos \theta, \sin \theta)\) changes quadrant.
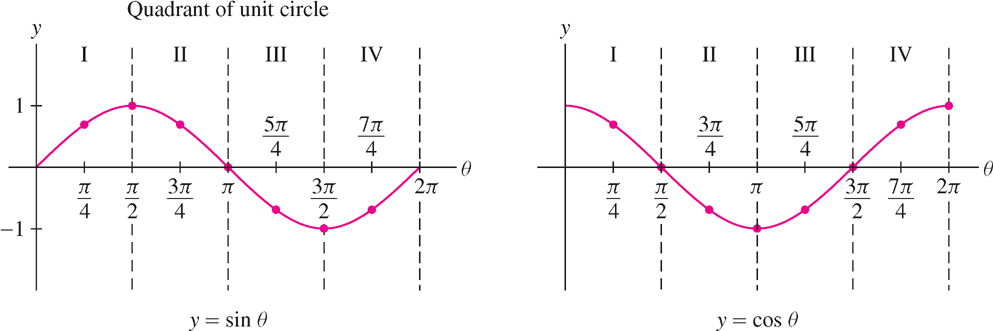
We often write \(\sin x\) and \(\cos x\), using \(x\) instead of \(\theta\). Depending on the application, we may think of \(x\) as an angle or simply as a real number.
A function \(f(x)\) is called periodic with period \(T\) if \(f(x + T) = f(x)\) (for all \(x\)) and \(T\) is the smallest positive number with this property. The sine and cosine functions are periodic with period \(T = 2\pi \) (Figure 1.46) because the radian measures \(x\) and \(x + 2\pi k\) correspond to the same point on the unit circle for any integer \(k\):
\[ \sin x = \sin(x + 2\pi k),\quad \cos x = \cos(x + 2\pi k) \]

28
There are four other standard trigonometric functions, each defined in terms of sin x and cos x or as ratios of sides in a right triangle (Figure 1.47):

\[\boxed{ \begin{array}{lclc} \text{Tangent:}&\tan x=\dfrac{\sin x}{\cos x}=\dfrac{b}{a},\quad&\text{Cotangent:}&\cot x=\dfrac{\cos x}{\sin x}=\dfrac{a}{b}\\[5pt] \text{Secant:}&\sec x=\dfrac{1}{\cos x}=\dfrac{c}{a},\quad&\text{Cosecant:}&\csc x=\dfrac{1}{\sin x}=\dfrac{c}{b} \end{array} } \]
These functions are periodic (Figure 1.48): \(y = \tan x\) and \(y = \cot x\) have period \(\pi \); \(y = \sec x\) and \(y = \csc x\) have period \(2\pi \) (see Exercise 55).

EXAMPLE 2 Computing Values of Trigonometric Functions
Find the values of the six trigonometric functions at \(x = \frac{4\pi}{3}\).
Solution The point \(P\) on the unit circle corresponding to the angle \(x =\frac{4\pi}{3}\) lies opposite the point with angle \(\frac{\pi}{3}\) (Figure 1.49). Thus, we see that (refer to Table 2)
\[ \sin\frac{4\pi}{3} = -\sin\frac{\pi}{3}=-\frac{\sqrt{3}}{2}\quad\text{and}\quad\cos\frac{4\pi}{3}=-\cos\frac{\pi}{3}=-\frac{1}{2} \]
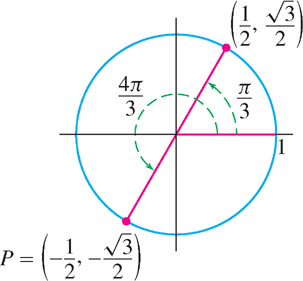
The remaining values are
\begin{align*} \tan\frac{4\pi}{3}&= \frac{\sin\frac{4\pi}{3}}{\cos\frac{4\pi}{3}}=\frac{-\frac{\sqrt{3}}{2}}{-\frac{1}{2}}=\sqrt{3},& \cot\frac{4\pi}{3}&=\frac{\cos\frac{4\pi}{3}}{\sin\frac{4\pi}{3}}=\frac{\sqrt{3}}{3}\\ \sec\frac{4\pi}{3}&=\frac{1}{\cos\frac{4\pi}{3}}=\frac{1}{-\frac{1}{2}}=-2,&\csc\frac{4\pi}{3}&=\frac{1}{\sin\frac{4\pi}{3}}=-\frac{2\sqrt{3}}{3} \end{align*}
EXAMPLE 3
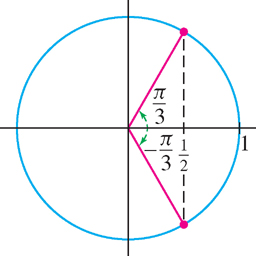
Find the angles \(x\) such that \(\sec x = 2\).
Solution Because \(\sec x = \frac{1}{\cos x}\), we must solve \(\cos x=\frac{1}{2}\). From Figure 1.50 we see that \(x=\frac{\pi}{3}\) and \(x=-\frac{\pi}{3}\) are solutions. We may add any integer multiple of \(2\pi \), so the general solution is \(x=\frac{\pi}{3}+2\pi k\) for any integer \(k\).
EXAMPLE 4 Trigonometric Equation
Solve \(\sin 4x + \sin 2x = 0\) for \(x \in [0, 2\pi )\).
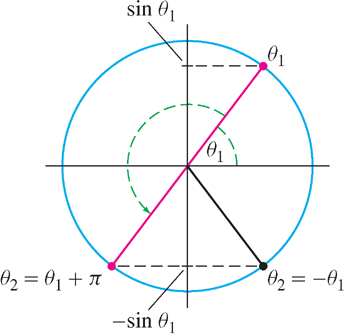
Solution We must find the angles \(x\) such that \(\sin 4x = -\sin 2x\). First, let’s determine when angles \(\theta_{1}\) and \(\theta_{2}\) satisfy \(\sin \theta_{2} = -\sin \theta_{1}\). Figure 1.51 shows that this occurs if \(\theta_{2} = -\theta_{1}\) or \(\theta_{2} = \theta_{1} + \pi \). Because the sine function is periodic with period \(2\pi \),
\[ \sin\theta_2=-\sin\theta_1\Leftrightarrow\theta_2 = -\theta_1+2\pi k\text{ or }\theta_2 = \theta_1 + \phi + 2\pi k \]
where \(k\) is an integer. Taking \(\theta_{2} = 4x\) and \(\theta_{1} = 2x\), we see that
\[ \sin 4x=-\sin 2x\Leftrightarrow 4x = -2x+2\pi k\text{ or }4x = 2x + \phi + 2\pi k \]
29
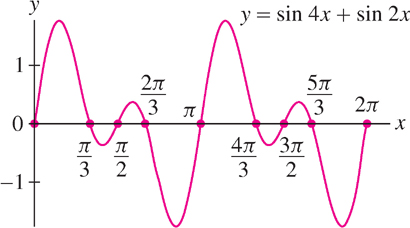
The first equation gives \(6x = 2\pi k\) or \(x = (\frac{\pi}{3})k\) and the second equation gives \(2x = \pi + 2\pi k\) or \(x = \frac{\pi}{2} + \pi k\). We obtain eight solutions in \([0, 2\pi )\) (Figure 1.52):
\[ x=0,\frac{\pi}{3},\frac{2\pi}{3},\pi,\frac{4\pi}{3},\frac{5\pi}{3} \quad\text{and}\quad x=\frac{\pi}{2},\frac{3\pi}{2} \]
EXAMPLE 5
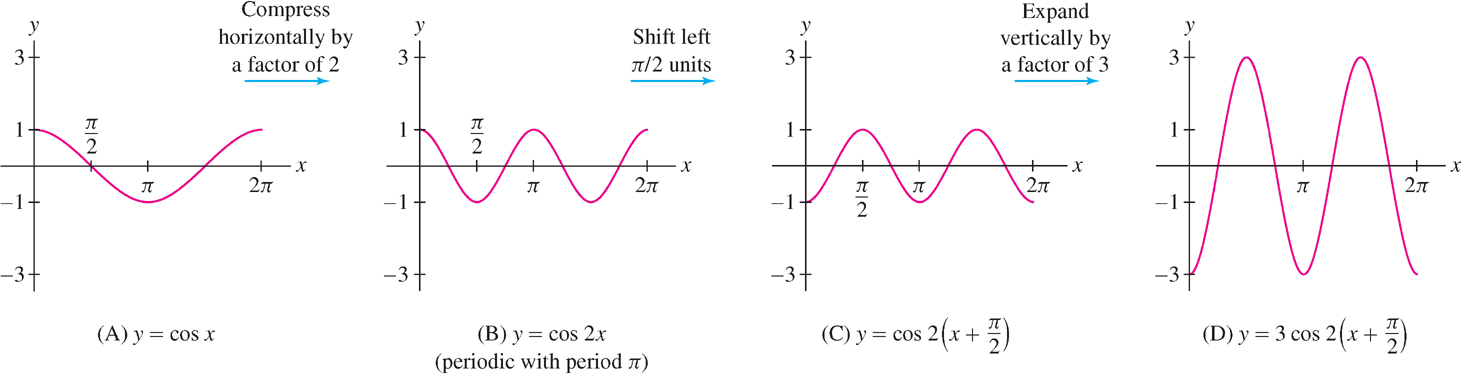
CAUTION To shift the graph of \(y = \cos 2x\) to the left \(\frac{\pi}{2}\) units, we must replace \(x\) by \(x+\frac{\pi}{2}\) to obtain \(\cos(2(x+\frac{\pi}{2}))\). It is incorrect to take \(\cos(2x+\frac{\pi}{2})\).
Sketch the graph of \(f(x)=3\cos(2(x+\frac{\pi}{2}))\) over \([0, 2\pi ]\).
Solution The graph is obtained by scaling and shifting the graph of \(y = \cos x\)
in three steps (Figure 1.53):
- Compress horizontally by a factor of \(2\): \(y=\cos 2x\)
- Shift to the left \(\frac{\pi}{2}\) units: \(y=\cos\left(2\left(x+\frac{\pi}{2}\right)\right)\)
- Expand vertically by a factor of \(3\): \(y=3\cos\left(2\left(x+\frac{\pi}{2}\right)\right)\)
1.4.1 Trigonometric Identities
A key feature of trigonometric functions is that they satisfy a large number of identities. First and foremost, sine and cosine satisfy a fundamental identity, which is equivalent to the Pythagorean Theorem:
The expression \( (sin x)^{k}\) is usually denoted \( sin^{k} x\). For example, \(sin^{2}x\) is the square of \(sin x\). We use similar notation for the other trigonometric functions.
\[ \boxed{\sin^2x+\cos^2x=1}\tag{1} \]
Equivalent versions are obtained by dividing Eq. (1) by \(\cos^{2}x\) or \(\sin^{2}x\):
\[ \boxed{\tan^2x+1=\sec^2x,\quad 1+\cot^2x=\csc^2x}\tag{2} \]
30
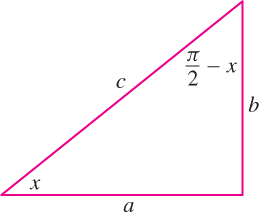
Here is a list of some other commonly used identities. The identities for complementary angles are justified by Figure 1.54.
Basic Trigonometric Identities
\[ \begin{array}{ll} \text{Complementary angles:}&\sin\left(\frac{\pi}{2}-x\right)=\cos x,\quad\cos\left(\frac{\pi}{2}-x\right)=\sin x\\[10pt] \text{Addition Formulas:}&\sin(x+y)=\sin x\cos y + \cos x \sin y \\ &\cos(x+y)=\cos x\cos y- \sin x \sin y\\[10pt] \text{Double-angle formulas:}&\sin^2x = \frac{1}{2}(1-\cos2x),\quad\cos^2x=\frac{1}{2}(1+\cos2x)\\ &\cos2x=\cos^2x-\sin^2x,\quad\sin2x=2\sin x\cos x\\[10pt] \text{Shift formulas:}&\sin\left(x+\frac{\pi}{2}\right)=\cos x,\quad \cos\left(x+\frac{\pi}{2}\right)=-\sin x \end{array} \]
EXAMPLE 6
Suppose that \(\cos\theta=\frac{2}{5}\). Calculate \(\tan \theta\) in the following two cases:
(a) \(0<\theta<\frac{\pi}{2}\) and (b) \(\pi < \theta < 2\pi \).
Solution First, using the identity \(\cos^{2}\theta + \sin^{2}\theta = 1\), we obtain
\[ \sin\theta=\pm\sqrt{1-\cos\theta}=\pm\sqrt{1-\frac{4}{2}5}=\pm\frac{\sqrt{21}}{5} \]
(a) If \(0<\theta<\frac{\pi}{2}\), then \(\sin \theta\) is positive and we take the positive square root:
\[ \tan\theta = \frac{\sin\theta}{\cos\theta}=\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}=\frac{\sqrt{21}}{2} \]
To visualize this computation, draw a right triangle with angle \(\theta\) such that \(\cos\theta=\frac{2}{5}\) as in Figure 1.55. The opposite side then has length \(\sqrt{5^2-2^2}=\sqrt{21}\) by the Pythagorean Theorem.
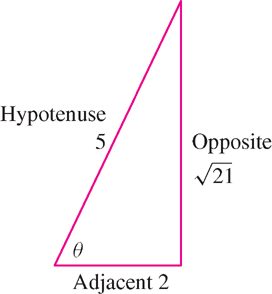
(b) If \(\pi < \theta < 2\pi \), then \(\sin \theta\) is negative and \(\tan\theta=-\frac{\sqrt{21}}{2}\).
We conclude this section by quoting the Law of Cosines (Figure 1.56), which is a generalization of the Pythagorean Theorem (see Exercise 58).
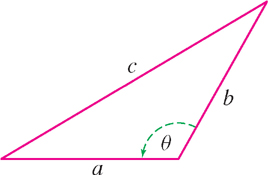
THEOREM 1 Law of Cosines
If a triangle has sides \(a\), \(b\), and \(c\), and \(\theta\) is the angle opposite side \(c\), then
\[ \boxed{c^2=a^2+b^2-2ab\cos\theta} \]
If \(\theta = 90^{\circ}\), then \(\cos \theta = 0\) and the Law of Cosines reduces to the Pythagorean Theorem.
1.4.2 Section 1.4 Summary
31
- An angle of \(\theta\) radians subtends an arc of length \(\theta r\) on a circle of radius \(r\).
- To convert from radians to degrees, multiply by \(\frac{180}{\pi}\) .
- To convert from degrees to radians, multiply by \(\frac{\pi}{180}\).
- Unless otherwise stated, all angles in this text are given in radians.
- The functions \(\cos \theta\) and \(\sin \theta\) are defined in terms of right triangles for acute angles and as coordinates of a point on the unit circle for general angles (Figure 1.57):
\[ \boxed{ \sin\theta=\dfrac{b}{c}=\dfrac{\text{opposite}}{\text{hypotenuse}},\quad \cos\theta=\dfrac{a}{c}=\dfrac{\text{adjacent}}{\text{hypotenuse}}} \]

- Basic properties of sine and cosine:
\[ \begin{array}{lll} \text{Periodicity:}&\sin(\theta+2\pi)=\sin\theta,&\cos(\theta+2\pi)=\cos\theta\\ \text{Parity:}&\sin(-\theta)=-\sin\theta,&\cos(-\theta)=\cos\theta\\ \text{Basic identity}&\sin^2\theta+\cos^2\theta=1& \end{array} \]
- The four additional trigonometric functions:
\[ \tan\theta=\frac{\sin\theta}{\cos\theta},\quad \cot\theta=\frac{\cos\theta}{\sin\theta},\quad \sec\theta=\frac{1}{\cos\theta},\quad \csc\theta=\frac{1}{\sin\theta} \]